Adaptive time-space algorithms for the simulation of multi-scale reaction waves with error control

Marc Massot (CMAP Paris)

Numerical simulations of multi-scale phenomena are commonly used for modeling purposes in many applications such as combustion, chemical vapor deposition, or air pollution modeling. These models raise several difficulties created by the high number of unknowns, the wide range of temporal scales due to detailed chemical kinetic mechanisms, as well as steep spatial gradients associated with very localized fronts of high chemical activity. Furthermore, a natural stumbling block to perform 3D simulations with all scales resolution is either the unreasonably small time step due to stability requirements or the unreasonable memory requirements for implicit methods. In this work, we introduce a new resolution strategy for multi-scale reaction waves based mainly on time operator splitting and space adaptive multiresolution. It considers high order time integration methods for reaction, diffusion and convection problems, in order to build a time operator splitting scheme that exploits efficiently the special features of each problem. Based on theoretical studies of numerical analysis, such a strategy leads to a splitting time step which is not restricted neither by fast scales in the source term nor by restrictive stability limits of diffusive or convective steps, but only by the physics of the phenomenon. Moreover, this splitting time step is dynamically adapted taking into account a posteriori error estimates, carefully computed by a second embedded and economic splitting method. The main goal is then to perform computationally very efficient as well as accurate in time and space simulations of the complete dynamics of multi-scale phenomena under study, considering large simulation domains with conventional computing resources and splitting time steps purely dictated by the physics of the phenomenon and not by any stability constraints associated with mesh size or source time scales. Applications will be presented in the fields of combustion waves and plasma discharges dynamics. We will also briefly address the question of parallelism as well as the coupling with a hydrodynamics solver.

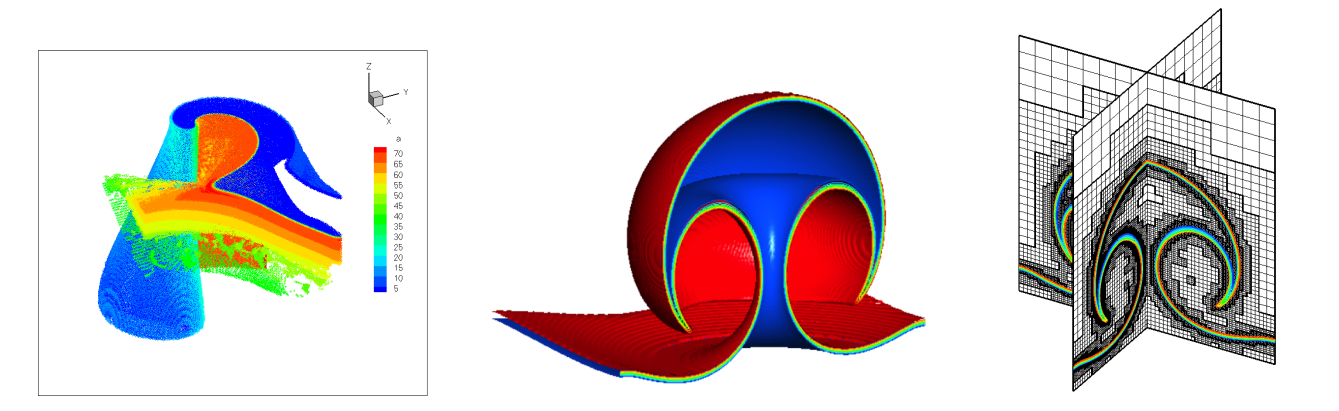
Left: Simulation of scroll waves using Belousov-Zhabotinsky model with detailed mechanism in 3D, Right: Simulation of the interaction of a premixed flame front with a toroidal vortex in 3D and mesh adaptation (Ph.D. M. Duarte).

[1] H. Leclerc, L. Séries, L. Gouarin, T. Dumont, M.A. N’Guessan, M. Massot, Multiresolution, efficiency, paralelism, nice APIs…best friend forever! NASA Technical Memorandum, Proceedings of the Summer Program 2018 at NASA Ames Research Center, Advanced Supercomputing Division (2018) 1-12

[2] S. Descombes, M. Duarte, T. Dumont, T. Guillet, V. Louvet, M. Massot, Task-based adaptive multiresolution for time-space multi-scale reaction-diffusion systems on multi-core architectures, SMAI - JCM, Vol. 3 (2017) 29-51

[3] M. Duarte, Z. Bonaventura, M. Massot, and A. Bourdon, A numerical strategy to discretize and solve Poisson equation on dynamically adapted multiresolution grids for time-dependent streamer discharge simulation, Journal of Computational Physics, 289 (2015) 129-148

[4] S. Descombes, M. Duarte, T. Dumont, F. Laurent, V. Louvet, M. Massot, Analysis of operator splitting in the non-asymptotic regime for nonlinear reaction diffusion equations. Application to the dynamics of premixed flames, SIAM Journal of Numerical Analysis, Vol. 52, No. 3 (2014) 1311-1334

[5] M. Duarte, S. Descombes, C. Tenaud, S. Candel, M. Massot, Time-space adaptive numerical methods for the simulation of combustion fronts. Combustion and Flame, Vol. 160, No. 6 (2013) 1083-1101

[6] T. Dumont, M. Duarte, S. Descombes, M.-A. Dronne, M. Massot, V. Louvet, Simulation of human ischemic stroke in realistic 3D geometry: a numerical strategy, à paraître dans Communications in Nonlinear Science and Numerical Simulation, Vol. 18, Issue 6 (2013) 1539-1557

[7] M. Duarte, Z. Bonaventura, M. Massot, A. Bourdon, S. Descombes, T. Dumont, A new numerical strategy with space-time adaptivity and error control for multi-scale streamer discharge simulations, Journal of Computational Physics, 231, 3 (2012) 1002-1019

[8] M. Duarte, M. Massot, S. Descombes, C. Tenaud, T. Dumont, V. Louvet, and F. Laurent. New resolution strategy for multi-scale reaction waves using time operator splitting, space adaptive multi-tiresolution and dedicated high order implicit/explicit time integrators. SIAM J. Sci. Comput., 34, 1 (2012) 76-104

[9] S. Descombes, M. Duarte, T. Dumont, V. Louvet, and M. Massot. Adaptive time splitting method for multi-scale evolutionary PDEs. Confluentes Mathematici, Numéro Spécial en hommage à Michelle Schatzman, Vol. 3, No. 3 (2011) 1-31